- 5.1. Score terminology
- 5.1.1. What is a score?
- 5.1.2. Score constraint signum (positive or negative)
- 5.1.3. Score constraint weight
- 5.1.4. Score level
- 5.1.5. Pareto scoring (AKA multi-objective optimization scoring)
- 5.1.6. Combining score techniques
- 5.1.7. The Score interface
- 5.1.8. Avoid floating point numbers in score calculation
- 5.2. Choose a Score definition
- 5.3. Calculate the Score
- 5.4. Score calculation performance tricks
- 5.4.1. Overview
- 5.4.2. Average calculation count per second
- 5.4.3. Incremental score calculation (with delta's)
- 5.4.4. Avoid calling remote services during score calculation
- 5.4.5. Pointless constraints
- 5.4.6. Build-in hard constraint
- 5.4.7. Other performance tricks
- 5.4.8. Score trap
- 5.4.9. stepLimit benchmark
- 5.4.10. Fairness score constraints
- 5.5. Reusing the score calculation outside the Solver
Every initialized Solution has a score. That score is an objective way to compare 2
solutions: the solution with the higher score is better. The Solver aims to find the
Solution with the highest Score of all possible solutions. The
best solution is the Solution with the highest Score
that Solver has encountered during solving, which might be the optimal
solution.
Planner cannot automatically know which Solution is best for your business, so you need
to tell it how to calculate the score of a given Solution according to your business needs.
There are multiple score techniques that you can use and combine:
Maximize or minimize a constraint: score constraint signum (positive or negative)
Put a cost/profit on constraints: score constraint weight
Prioritize constraints: score level
Pareto scoring
All score techniques are based on constraints. Such a constraint can be a simple pattern (such as Maximize the apple harvest in the solution) or a more complex pattern. A positive constraint is a constraint you're trying to maximize. A negative constraint is a constraint you're trying to minimize.
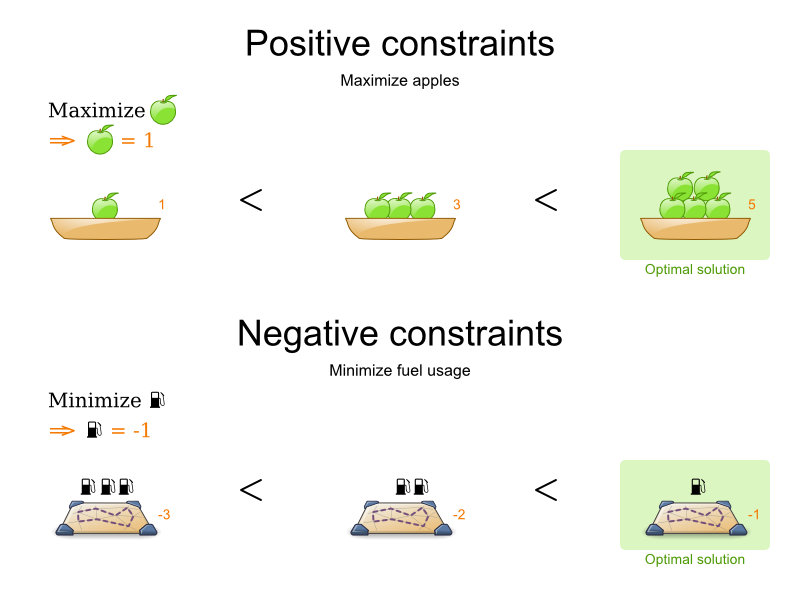
Notice in the image above, that the optimal solution always has the highest score, regardless if the constraints are positive or negative.
Most planning problems have only negative constraints and therefore have a negative score. In that case, the score is usually the sum of the weight of the negative constraints being broken, with a perfect score of 0. This explains why the score of a solution of 4 queens is the negative (and not the positive!) of the number of queen couples which can attack each other.
Negative and positive constraints can be combined, even in the same score level.
Note
Don't presume your business knows all its score constraints in advance. Expect score constraints to be added or changed after the first releases.
When a constraint activates (because the negative constraint is broken or the positive constraint is fulfilled) on a certain planning entity set, it is called a constraint match.
Not all score constraints are equally important. If breaking one constraint is equally bad as breaking another constraint x times, then those 2 constraints have a different weight (but they are in the same score level). For example in vehicle routing, you can make 2 "unhappy driver" constraint matches count as much as 1 "fuel tank usage" constraint match:
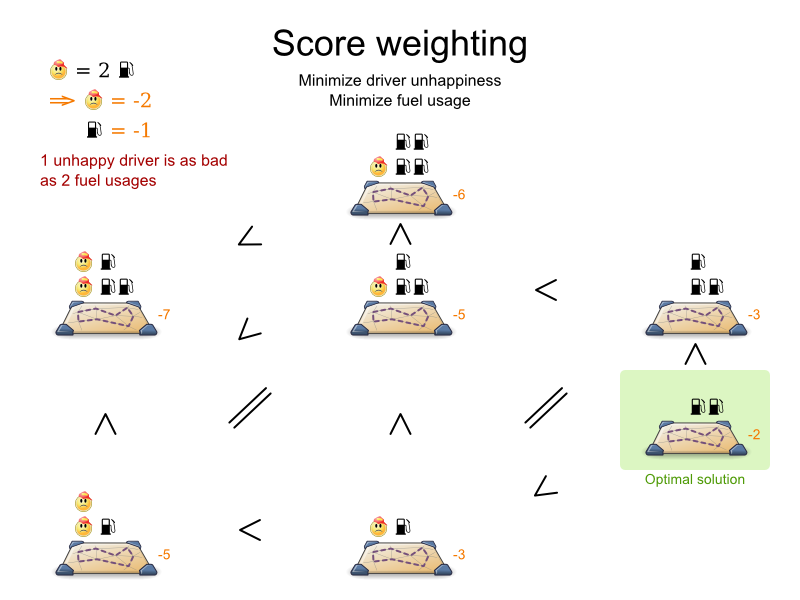
Score weighting is often used in use cases where you can put a price tag on everything. In that case, the positive constraints maximize revenue and the negative constraints minimize expenses: together they maximize profit. Alternatively, score weighting is also often used to create social fairness. For example: nurses that request a free day on New Year's eve pay a higher weight than on a normal day.
The weight of a constraint match can be dynamically based on the planning entities involved. For example in
cloud balance: the weight of the soft constraint match for an active Computer is the
cost of that Computer.
Sometimes a score constraint outranks another score constraint, no matter how many times the other is broken. In that case, those score constraints are in different levels. For example: a nurse cannot do 2 shifts at the same time (due to the constraints of physical reality), this outranks all nurse happiness constraints.
Most use cases have only 2 score levels: hard and soft. When comparing 2 scores, they are compared lexicographically: the first score level gets compared first. If those differ, the others score levels are ignored. For example: a score that breaks 0 hard constraints and 1000000 soft constraints is better than a score that breaks 1 hard constraint and 0 soft constraints.
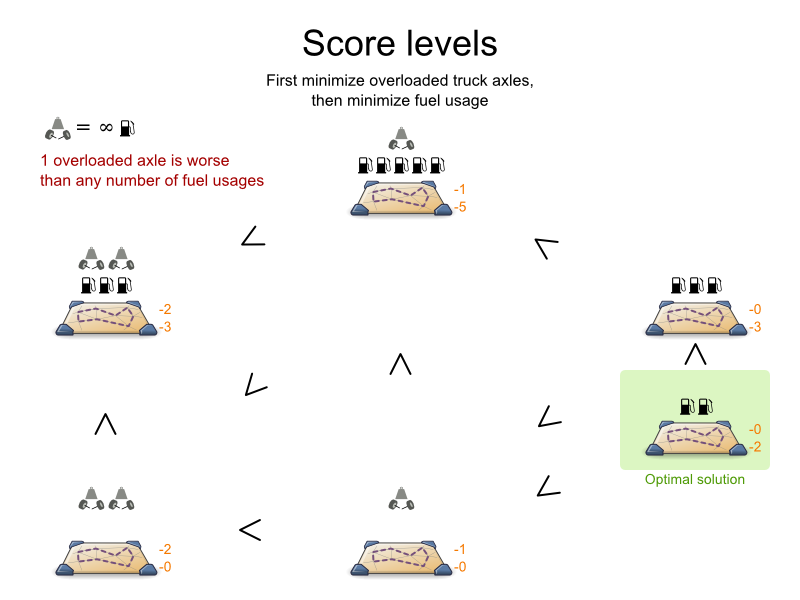
Score levels often employ score weighting per level. In such case, the hard constraint level usually makes the solution feasible and the soft constraint level maximizes profit by weighting the constraints on price.
Don't use a big constraint weight when your business actually wants different score levels. That hack, known as score folding, is broken:
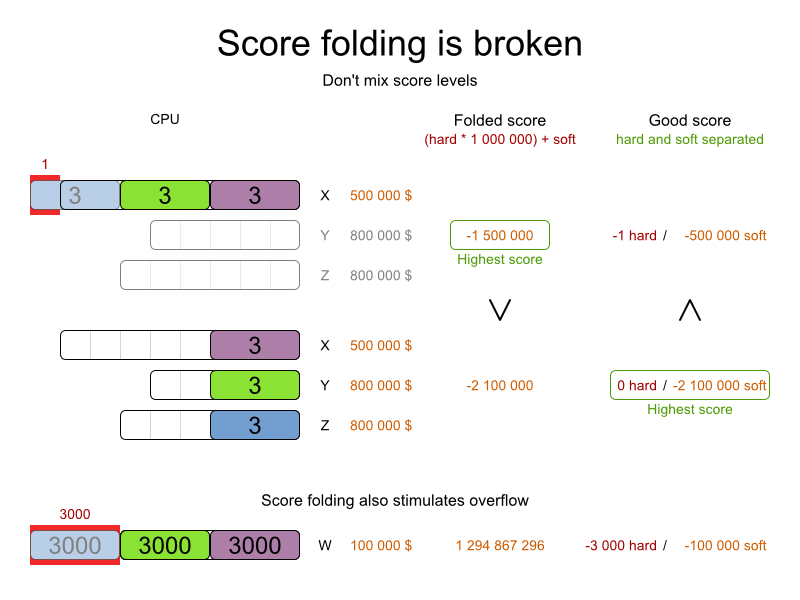
Note
Your business will probably tell you that your hard constraints all have the same weight, because they
cannot be broken (so their weight does not matter). This is not true and it could create a score trap. For example in cloud balance: if a Computer has 7 CPU
too little for its Processes, then it must be weighted 7 times as much as if it had only 1
CPU too little. This way, there is an incentive to move a Process with 6 CPU or less away
from that Computer.
3 or more score levels is supported. For example: a company might decide that profit outranks employee satisfaction (or visa versa), while both are outranked by the constraints of physical reality.
Far less common is the use case of pareto optimization, which is also known under the more confusing term multi-objective optimization. In pareto scoring, score constraints are in the same score level, yet they are not weighted against each other. When 2 scores are compared, each of the score constraints are compared individually and the score with the most dominating score constraints wins. Pareto scoring can even be combined with score levels and score constraint weighting.
Consider this example with positive constraints, where we want to get the most apples and oranges. Since it's impossible to compare apples and oranges, we can't weight them against each other. Yet, despite that we can't compare them, we can state that 2 apples are better then 1 apple. Similarly, we can state that 2 apples and 1 orange are better than just 1 orange. So despite our inability to compare some Scores conclusively (at which point we declare them equal), we can find a set of optimal scores. Those are called pareto optimal.
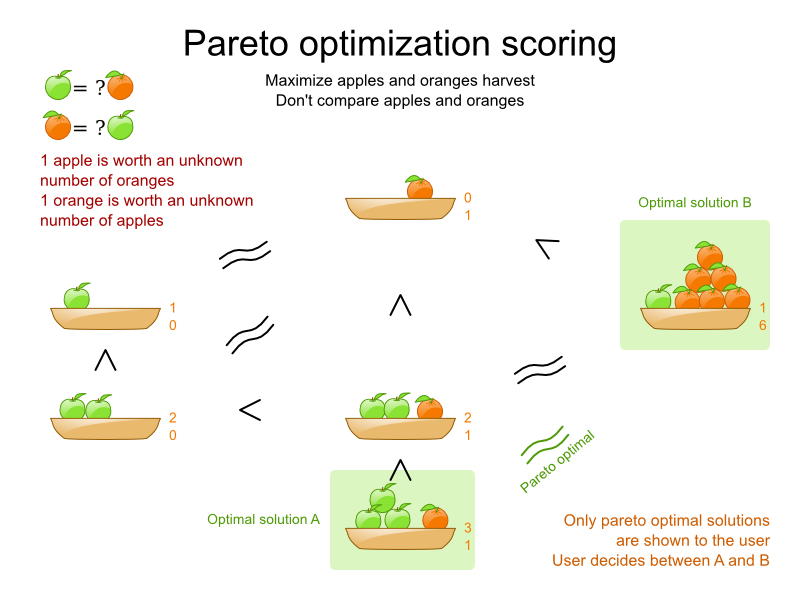
Scores are considered equal far more often. It's left up to a human to choose the better out of a set of best solutions (with equal scores) found by Planner. In the example above, the user must choose between solution A (3 apples and 1 orange) and solution B (1 apples and 6 oranges). It's guaranteed that Planner has not found another solution which has more apples or more oranges or even a better combination of both (such as 2 apples and 3 oranges).
To implement pareto scoring in Planner, implement a custom
ScoreDefinition and Score (and replace the
BestSolutionRecaller). Future versions will provide out-of-the-box support.
Note
A pareto Score's method compareTo is not transitive because it does
a pareto comparison. For example: 2 apples is greater than 1 apple. 1 apples is equal to 1 orange. Yet, 2 apples
are not greater than 1 orange (but actually equal). Pareto comparison violates the contract of the interface
java.lang.Comparable's method compareTo, but Planner's systems are
pareto comparison safe, unless explicitly stated otherwise in this documentation.
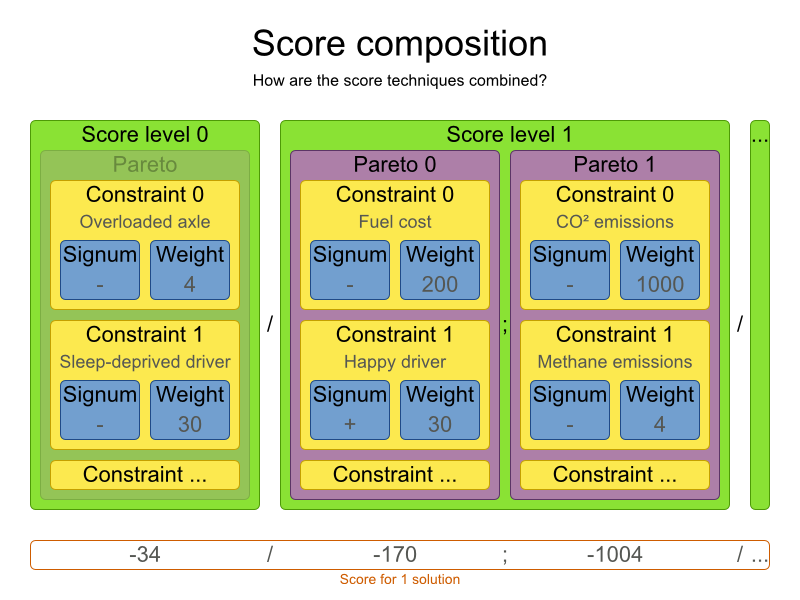
All the score techniques mentioned above, can be combined seamlessly:
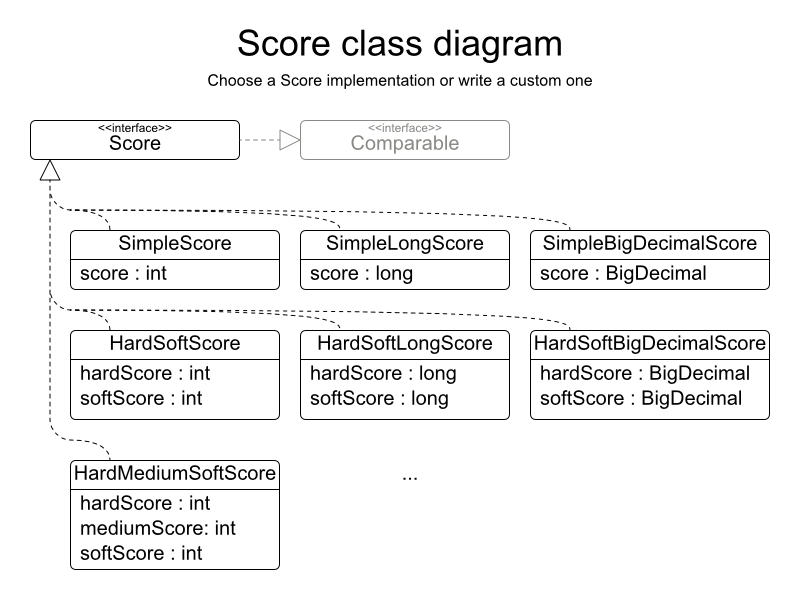
A score is represented by the Score interface, which naturally extends
Comparable:
public interface Score<...> extends Comparable<...> {
...
}
The Score implementation to use depends on your use case. Your score might not
efficiently fit in a single long value. Planner has several build-in Score
implementations, but you can implement a custom Score too. Most use cases tend to use the
build-in HardSoftScore.
The Score implementation (for example HardSoftScore) must be the same
throughout a Solver runtime. The Score implementation is configured in the
solver configuration as a ScoreDefinition:
<scoreDirectorFactory>
<scoreDefinitionType>HARD_SOFT</scoreDefinitionType>
...
</scoreDirectorFactory>
Avoid the use of float and double for score calculation. Use
BigDecimal instead.
Floating point numbers (float and double) cannot represent a decimal
number correctly. For example: a double cannot hold the value 0.05
correctly. Instead, it holds the nearest representable value. Arithmetic (including addition and subtraction) with
floating point numbers, especially for planning problems, leads to incorrect decisions:
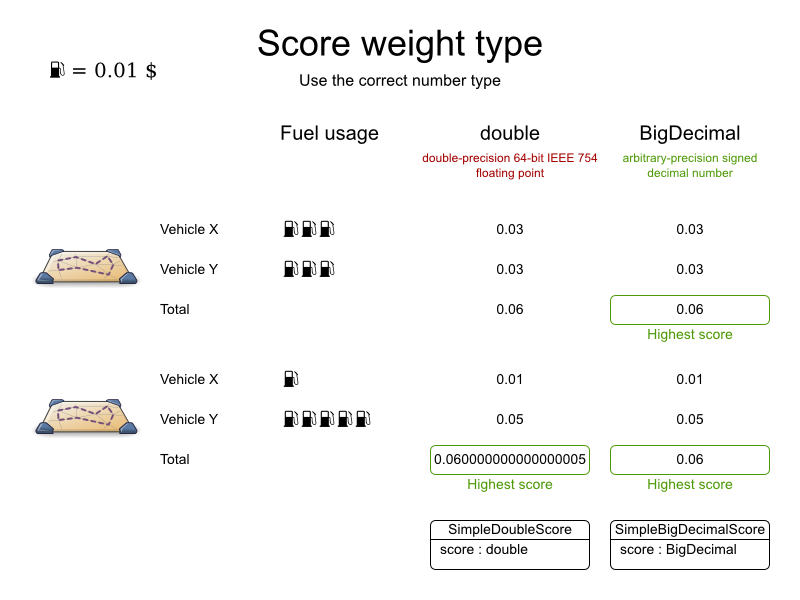
Additionally, floating point number addition is not associative:
System.out.println( ((0.01 + 0.02) + 0.03) == (0.01 + (0.02 + 0.03)) ); // returns false
This leads to score corruption.
Decimal numbers (BigDecimal) have none of these problems.
Note
BigDecimal arithmetic is considerably slower than int, long or
double arithmetic. In experiments we've seen the average calculation count get divided by
5.
Therefore, in some cases, it can be worthwhile to multiply all numbers for a single
score weight by a plural of ten (for example 1000), so the score weight fits in an
int or long.
Each Score implementation also has a ScoreDefinition implementation. For
example: SimpleScore is definied by SimpleScoreDefinition.
A SimpleScore has a single int value, for example
-123. It has a single score level.
<scoreDirectorFactory>
<scoreDefinitionType>SIMPLE</scoreDefinitionType>
...
</scoreDirectorFactory>
Variants of this scoreDefinitionType:
SIMPLE_LONG: UsesSimpleLongScorewhich has alongvalue instead of anintvalue.SIMPLE_DOUBLE: UsesSimpleDoubleScorewhich has adoublevalue instead of anintvalue. Not recommended to use.SIMPLE_BIG_DECIMAL: UsesSimpleBigDecimalScorewhich has aBigDecimalvalue instead of anintvalue.
A HardSoftScore has a hard int value and a soft int
value, for example -123hard/-456soft. It has 2 score levels (hard and soft).
<scoreDirectorFactory>
<scoreDefinitionType>HARD_SOFT</scoreDefinitionType>
...
</scoreDirectorFactory>
Variants of this scoreDefinitionType:
HARD_SOFT_LONG: UsesHardSoftLongScorewhich haslongvalues instead ofintvalues.HARD_SOFT_DOUBLE: UsesHardSoftDoubleScorewhich hasdoublevalues instead ofintvalues. Not recommended to use.HARD_SOFT_BIG_DECIMAL: UsesHardSoftBigDecimalScorewhich hasBigDecimalvalues instead ofintvalues..
A HardMediumSoftScore which has a hard int value, a medium
int value and a soft int value, for example
-123hard/-456medium/-789soft. It has 3 score levels (hard, medium and soft).
<scoreDirectorFactory>
<scoreDefinitionType>HARD_MEDIUM_SOFT</scoreDefinitionType>
...
</scoreDirectorFactory>
A BendableScore has a configurable number of score levels. It has an array of hard
int values and an array of soft int value, for example 2 hard levels and 3
soft levels for a score -123/-456/-789/-012/-345. The number of hard and soft score levels
needs to be set at configuration time, it's not flexible to change during solving.
<scoreDirectorFactory>
<scoreDefinitionType>BENDABLE</scoreDefinitionType>
<bendableHardLevelCount>2</bendableHardLevelCount>
<bendableSoftLevelCount>3</bendableSoftLevelCount>
...
</scoreDirectorFactory>
The ScoreDefinition interface defines the score representation.
To implement a custom Score, you'll also need to implement a custom ScoreDefinition.
Extend AbstractScoreDefinition (preferable by copy pasting
HardSoftScoreDefinition or SimpleScoreDefinition) and start from
there.
Then hook your custom ScoreDefinition in your
SolverConfig.xml:
<scoreDirectorFactory>
<scoreDefinitionClass>...MyScoreDefinition</scoreDefinitionClass>
...
</scoreDirectorFactory>
There are several ways to calculate the Score of a Solution:
Simple Java score calculation: implement a single Java method
Incremental Java score calculation: implement multiple Java methods
Drools score calculation: implement score rules
Every score calculation type can use any Score definition. For example, simple Java score calculation can
output a HardSoftScore.
All score calculation types are Object Orientated and can reuse existing Java code.
Important
The score calculation should be read-only: it should not change the planning entities or the problem facts in any way. For example, it must not call a setter method on a planning entity in a Drools score rule's RHS. This does not apply to logically inserted objects, which can be changed by the score rules who logically inserted them in the first place.
OptaPlanner will not recalculate the score of a Solution if it can predict it (unless
an environmentMode assertion is enabled). For example, after a winning
step is done, there is no need to calculate the score because that move was done and undone earlier. As a
result, there's no guarantee that such changes applied during score calculation are actually done.
A simple way to implement your score calculation in Java.
Advantages:
Plain old Java: no learning curve
Opportunity to delegate score calculation to an existing code base or legacy system
Disadvantages:
Slower and less scalable
Because there is no incremental score calculation
Just implement one method of the interface SimpleScoreCalculator:
public interface SimpleScoreCalculator<Sol extends Solution> {
Score calculateScore(Sol solution);
}
For example in n queens:
public class NQueensSimpleScoreCalculator implements SimpleScoreCalculator<NQueens> {
public SimpleScore calculateScore(NQueens nQueens) {
int n = nQueens.getN();
List<Queen> queenList = nQueens.getQueenList();
int score = 0;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
Queen leftQueen = queenList.get(i);
Queen rightQueen = queenList.get(j);
if (leftQueen.getRow() != null && rightQueen.getRow() != null) {
if (leftQueen.getRowIndex() == rightQueen.getRowIndex()) {
score--;
}
if (leftQueen.getAscendingDiagonalIndex() == rightQueen.getAscendingDiagonalIndex()) {
score--;
}
if (leftQueen.getDescendingDiagonalIndex() == rightQueen.getDescendingDiagonalIndex()) {
score--;
}
}
}
}
return SimpleScore.valueOf(score);
}
}
Configure it in your solver configuration:
<scoreDirectorFactory>
<scoreDefinitionType>...</scoreDefinitionType>
<simpleScoreCalculatorClass>org.optaplanner.examples.nqueens.solver.score.NQueensSimpleScoreCalculator</simpleScoreCalculatorClass>
</scoreDirectorFactory>
Alternatively, build a SimpleScoreCalculator instance at runtime and set it with the
programmatic API:
solverFactory.getSolverConfig().getScoreDirectorFactoryConfig.setSimpleScoreCalculator(simpleScoreCalculator);
A way to implement your score calculation incrementally in Java.
Advantages:
Very fast and scalable
Currently the fastest if implemented correctly
Disadvantages:
Hard to write
A scalable implementation heavily uses maps, indexes, ... (things the Drools rule engine can do for you)
You have to learn, design, write and improve all these performance optimizations yourself
Hard to read
Regular score constraint changes can lead to a high maintenance cost
Implement all the methods of the interface IncrementalScoreCalculator and extend the
class AbstractIncrementalScoreCalculator:
public interface IncrementalScoreCalculator<Sol extends Solution> {
void resetWorkingSolution(Sol workingSolution);
void beforeEntityAdded(Object entity);
void afterEntityAdded(Object entity);
void beforeVariableChanged(Object entity, String variableName);
void afterVariableChanged(Object entity, String variableName);
void beforeEntityRemoved(Object entity);
void afterEntityRemoved(Object entity);
Score calculateScore();
}
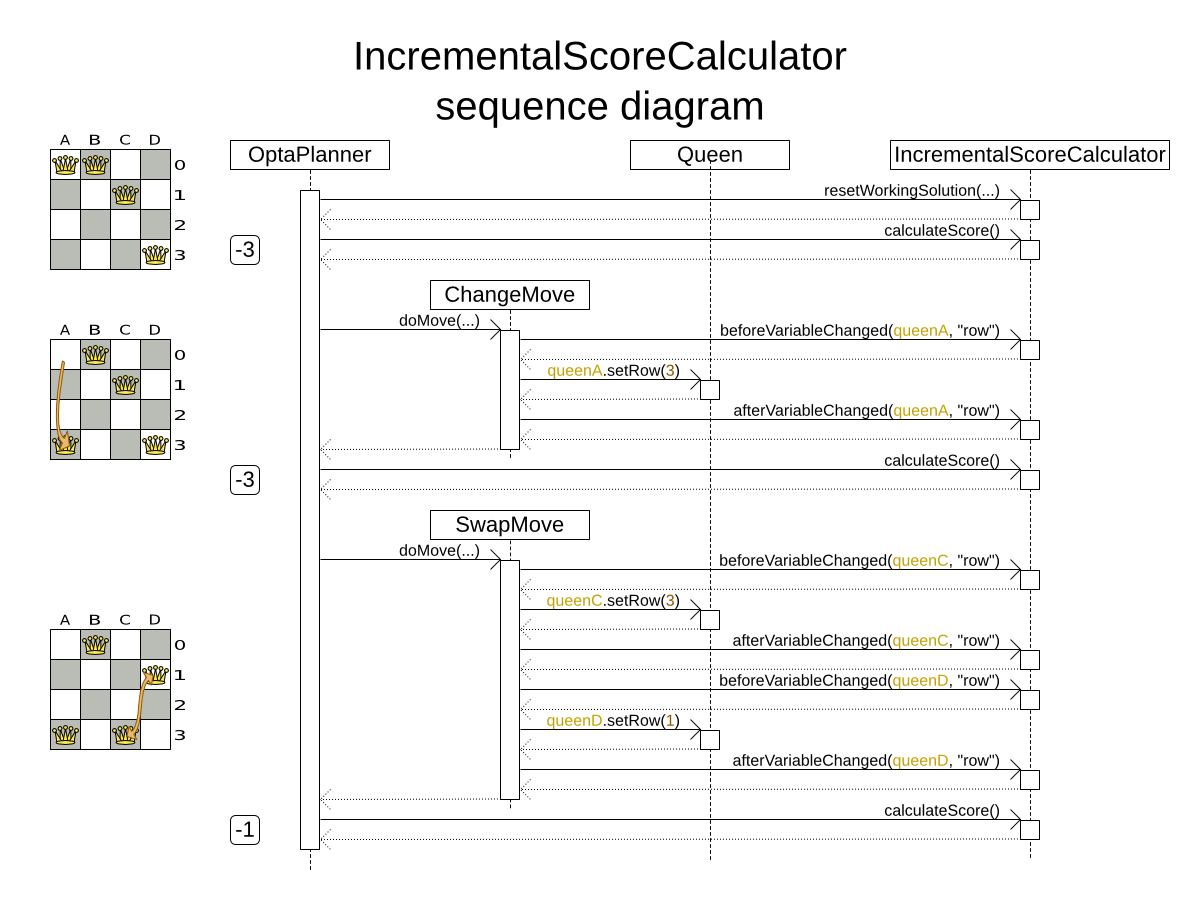
For example in n queens:
public class NQueensAdvancedIncrementalScoreCalculator extends AbstractIncrementalScoreCalculator<NQueens> {
private Map<Integer, List<Queen>> rowIndexMap;
private Map<Integer, List<Queen>> ascendingDiagonalIndexMap;
private Map<Integer, List<Queen>> descendingDiagonalIndexMap;
private int score;
public void resetWorkingSolution(NQueens nQueens) {
int n = nQueens.getN();
rowIndexMap = new HashMap<Integer, List<Queen>>(n);
ascendingDiagonalIndexMap = new HashMap<Integer, List<Queen>>(n * 2);
descendingDiagonalIndexMap = new HashMap<Integer, List<Queen>>(n * 2);
for (int i = 0; i < n; i++) {
rowIndexMap.put(i, new ArrayList<Queen>(n));
ascendingDiagonalIndexMap.put(i, new ArrayList<Queen>(n));
descendingDiagonalIndexMap.put(i, new ArrayList<Queen>(n));
if (i != 0) {
ascendingDiagonalIndexMap.put(n - 1 + i, new ArrayList<Queen>(n));
descendingDiagonalIndexMap.put((-i), new ArrayList<Queen>(n));
}
}
score = 0;
for (Queen queen : nQueens.getQueenList()) {
insert(queen);
}
}
public void beforeEntityAdded(Object entity) {
// Do nothing
}
public void afterEntityAdded(Object entity) {
insert((Queen) entity);
}
public void beforeVariableChanged(Object entity, String variableName) {
retract((Queen) entity);
}
public void afterVariableChanged(Object entity, String variableName) {
insert((Queen) entity);
}
public void beforeEntityRemoved(Object entity) {
retract((Queen) entity);
}
public void afterEntityRemoved(Object entity) {
// Do nothing
}
private void insert(Queen queen) {
Row row = queen.getRow();
if (row != null) {
int rowIndex = queen.getRowIndex();
List<Queen> rowIndexList = rowIndexMap.get(rowIndex);
score -= rowIndexList.size();
rowIndexList.add(queen);
List<Queen> ascendingDiagonalIndexList = ascendingDiagonalIndexMap.get(queen.getAscendingDiagonalIndex());
score -= ascendingDiagonalIndexList.size();
ascendingDiagonalIndexList.add(queen);
List<Queen> descendingDiagonalIndexList = descendingDiagonalIndexMap.get(queen.getDescendingDiagonalIndex());
score -= descendingDiagonalIndexList.size();
descendingDiagonalIndexList.add(queen);
}
}
private void retract(Queen queen) {
Row row = queen.getRow();
if (row != null) {
List<Queen> rowIndexList = rowIndexMap.get(queen.getRowIndex());
rowIndexList.remove(queen);
score += rowIndexList.size();
List<Queen> ascendingDiagonalIndexList = ascendingDiagonalIndexMap.get(queen.getAscendingDiagonalIndex());
ascendingDiagonalIndexList.remove(queen);
score += ascendingDiagonalIndexList.size();
List<Queen> descendingDiagonalIndexList = descendingDiagonalIndexMap.get(queen.getDescendingDiagonalIndex());
descendingDiagonalIndexList.remove(queen);
score += descendingDiagonalIndexList.size();
}
}
public SimpleScore calculateScore() {
return SimpleScore.valueOf(score);
}
}
Configure it in your solver configuration:
<scoreDirectorFactory>
<scoreDefinitionType>...</scoreDefinitionType>
<incrementalScoreCalculatorClass>org.optaplanner.examples.nqueens.solver.score.NQueensAdvancedIncrementalScoreCalculator</incrementalScoreCalculatorClass>
</scoreDirectorFactory>
Optionally, to get better output when the IncrementalScoreCalculator is corrupted in
environmentMode FAST_ASSERT or FULL_ASSERT, you can
overwrite the method buildScoreCorruptionAnalysis from
AbstractIncrementalScoreCalculator.
Implement your score calculation using the Drools rule engine. Every score constraint is written as one or more score rules.
Advantages:
Incremental score calculation for free
Because most DRL syntax uses forward chaining, it does incremental calculation without any extra code
Score constraints are isolated as separate rules
Easy to add or edit existing score rules
Flexibility to augment your score constraints by
Defining them in decision tables
Excel (XLS) spreadsheet
KIE Workbench WebUI
Translate them into natural language with DSL
Store and release in the KIE Workbench repository
Performance optimizations in future versions for free
In every release, the Drools rule engine tends to become faster.
Disadvantages:
DRL learning curve
Usage of DRL
Polyglot fear can prohibit the use of a new language such as DRL in some organizations
There are several ways to define where your score rules live.
This is the easy way: the score rule live in a DRL file which is a resource on the classpath. Just add
your score rules *.drl file in the solver configuration:
<scoreDirectorFactory>
<scoreDefinitionType>...</scoreDefinitionType>
<scoreDrl>/org/optaplanner/examples/nqueens/solver/nQueensScoreRules.drl</scoreDrl>
</scoreDirectorFactory>
You can add multiple <scoreDrl> entries if needed, but normally you'll define
all your score rules in 1 file.
Optionally, you can also set drools configuration properties but beware of backwards compatibility issues:
<scoreDirectorFactory>
...
<scoreDrl>/org/optaplanner/examples/nqueens/solver/nQueensScoreRules.drl</scoreDrl>
<kieBaseConfigurationProperties>
<drools.equalityBehavior>...</drools.equalityBehavior>
</kieBaseConfigurationProperties>
</scoreDirectorFactory>
If you prefer to build the KieBase yourself or if you're combining Planner with
KIE Workbench (formerly known as Guvnor), you can set the KieBase on the
SolverFactory before building the Solver:
solverFactory.getSolverConfig().getScoreDirectorFactoryConfig.setKieBase(kieBase);
Note
To be able to define your score rules in Drools Workbench, you'll want to:
Upload the optaplanner-core jar as a POJO model.
Add a global variable called
scoreHolder(see below).
Here's an example of a score constraint implemented as a score rule in a DRL file:
rule "multipleQueensHorizontal"
when
Queen($id : id, row != null, $i : rowIndex)
Queen(id > $id, rowIndex == $i)
then
scoreHolder.addConstraintMatch(kcontext, -1);
endThis score rule will fire once for every 2 queens with the same rowIndex. The
(id > $id) condition is needed to assure that for 2 queens A and B, it can only fire for
(A, B) and not for (B, A), (A, A) or (B, B). Let's take a closer look at this score rule on this solution of 4
queens:
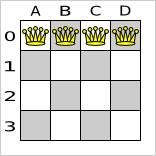
In this solution the multipleQueensHorizontal score rule will fire for 6 queen couples: (A, B), (A, C),
(A, D), (B, C), (B, D) and (C, D). Because none of the queens are on the same vertical or diagonal line, this
solution will have a score of -6. An optimal solution of 4 queens has a score of
0.
Note
Notice that every score rule will relate to at least 1 planning entity class (directly or indirectly though a logically inserted fact).
This is normal: it would be a waste of time to write a score rule that only relates to problem facts, as the consequence will never change during planning, no matter what the possible solution.
Note
The variable kcontext is a magic variable in Drools Expert. The scoreHolder's method
uses it to do incremental score calculation correctly and to create a ConstraintMatch
instance.
A ScoreHolder instance is asserted into the KieSession as a global
called scoreHolder. Your score rules need to (directly or indirectly) update that
instance.
global SimpleScoreHolder scoreHolder;
rule "multipleQueensHorizontal"
when
Queen($id : id, row != null, $i : rowIndex)
Queen(id > $id, rowIndex == $i)
then
scoreHolder.addConstraintMatch(kcontext, -1);
end
// multipleQueensVertical is obsolete because it is always 0
rule "multipleQueensAscendingDiagonal"
when
Queen($id : id, row != null, $i : ascendingDiagonalIndex)
Queen(id > $id, ascendingDiagonalIndex == $i)
then
scoreHolder.addConstraintMatch(kcontext, -1);
end
rule "multipleQueensDescendingDiagonal"
when
Queen($id : id, row != null, $i : descendingDiagonalIndex)
Queen(id > $id, descendingDiagonalIndex == $i)
then
scoreHolder.addConstraintMatch(kcontext, -1);
endMost use cases will also weigh their constraint types or even their matches differently, by using a specific weight for each constraint match.
Here's an example from CurriculumCourse, where assigning a Lecture to a
Room which is missing 2 seats is weighted equally bad as having 1 isolated
Lecture in a Curriculum:
global HardSoftScoreHolder scoreHolder;
// RoomCapacity: For each lecture, the number of students that attend the course must be less or equal
// than the number of seats of all the rooms that host its lectures.
// Each student above the capacity counts as 1 point of penalty.
rule "roomCapacity"
when
$room : Room($capacity : capacity)
$lecture : Lecture(room == $room, studentSize > $capacity, $studentSize : studentSize)
then
scoreHolder.addSoftConstraintMatch(kcontext, ($capacity - $studentSize));
end
// CurriculumCompactness: Lectures belonging to a curriculum should be adjacent
// to each other (i.e., in consecutive periods).
// For a given curriculum we account for a violation every time there is one lecture not adjacent
// to any other lecture within the same day.
// Each isolated lecture in a curriculum counts as 2 points of penalty.
rule "curriculumCompactness"
when
...
then
scoreHolder.addSoftConstraintMatch(kcontext, -2);
endPut the environmentMode in FULL_ASSERT (or
FAST_ASSERT) to detect corruption in the incremental score calculation. For more information, see the section about environmentMode. However, that will not
verify that your score calculator implements your score constraints as your business actually desires.
A piece of incremental score calculator code can be difficult to write and to review. Assert its correctness
by using a different implementation (for example a SimpleScoreCalculator) to do the assertions
triggered by the environmentMode. Just configure the different implementation as a
assertionScoreDirectorFactory:
<environmentMode>FAST_ASSERT</environmentMode>
...
<scoreDirectorFactory>
<scoreDefinitionType>...</scoreDefinitionType>
<scoreDrl>/org/optaplanner/examples/nqueens/solver/nQueensScoreRules.drl</scoreDrl>
<assertionScoreDirectorFactory>
<simpleScoreCalculatorClass>org.optaplanner.examples.nqueens.solver.score.NQueensSimpleScoreCalculator</simpleScoreCalculatorClass>
</assertionScoreDirectorFactory>
</scoreDirectorFactory>
This way, the scoreDrl will be validated by the
SimpleScoreCalculator.
The Solver will normally spend most of its execution time running the score calculation
(which is called in its deepest loops). Faster score calculation will return the same solution in less time with
the same algorithm, which normally means a better solution in equal time.
After solving a problem, the Solver will log the average calculation count per
second. This is a good measurement of Score calculation performance, despite that it is affected by non
score calculation execution time. It depends on the problem scale of the problem dataset. Normally, even for high
scale problems, it is higher than 1000, except when you're using
SimpleScoreCalculator.
Important
When improving your score calculation, focus on maximizing the average calculation count per second, instead of maximizing the best score. A big improvement in score calculation can sometimes yield little or no best score improvement, for example when the algorithm is stuck in a local or global optima. If you're watching the calculation count instead, score calculation improvements are far more visible.
Furthermore, watching the calculation count, allows you to remove or add score constraints, and still compare it with the original calculation count. Comparing the best score with the original would be wrong, because it's comparing apples and oranges.
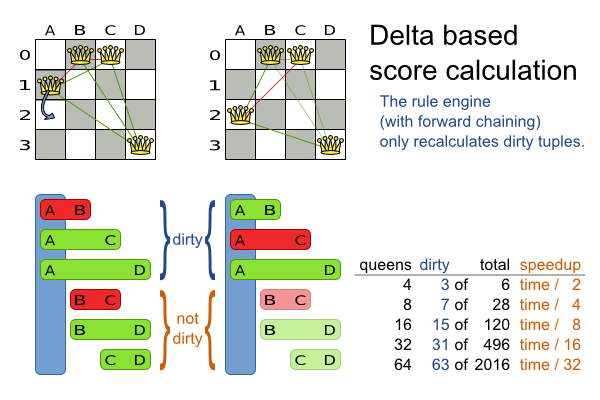
When a Solution changes, incremental score calculation (AKA delta based score
calculation), will calculate the delta with the previous state to find the new Score, instead
of recalculating the entire score on every solution evaluation.
For example, if a single queen A moves from row 1 to 2, it won't
bother to check if queen B and C can attack each other, since neither of them changed.
This is a huge performance and scalability gain. Drools score calculation gives you this huge scalability gain without forcing you to write a complicated incremental score calculation algorithm. Just let the Drools rule engine do the hard work.
Notice that the speedup is relative to the size of your planning problem (your n), making incremental score calculation far more scalable.
Do not call remote services in your score calculation (except if you're bridging
SimpleScoreCalculator to a legacy system). The network latency will kill your score calculation
performance. Cache the results of those remote services if possible.
If some parts of a constraint can be calculated once, when the Solver starts, and never
change during solving, then turn them into cached problem facts.
If you know a certain constraint can never be broken (or it is always broken), don't bother writing a score constraint for it. For
example in n queens, the score calculation doesn't check if multiple queens occupy the same column, because a
Queen's column never changes and every Solution starts
with each Queen on a different column.
Note
Don't go overboard with this. If some datasets don't use a specific constraint but others do, just return out of the constraint as soon as you can. There is no need to dynamically change your score calculation based on the dataset.
Instead of implementing a hard constraint, you can sometimes make it build-in too. For example: If
Lecture A should never be assigned to Room X, but it uses ValueRangeProvider
on Solution, the Solver will often try to assign it to Room X too (only to
find out that it breaks a hard constraint). Use filtered selection to
define that Course A should only be assigned a Room other than X.
This tends to give a good performance gain, not just because the score calculation is faster, but mainly because most optimization algorithms will spend less time evaluating unfeasible solutions.
Note
Don't go overboard with this. Many optimization algorithms rely on the freedom to break hard constraints when changing planning entities, to get out of local optima. There is a real risk of trading short term benefits for long term harm.
Verify that your score calculation happens in the correct
Numbertype. If you're making the sum ofintvalues, don't let Drools sum it in adoublewhich takes longer.For optimal performance, always use server mode (
java -server). We have seen performance increases of 50% by turning on server mode.For optimal performance, use the latest Java version. For example, in the past we have seen performance increases of 30% by switching from java 1.5 to 1.6.
Always remember that premature optimization is the root of all evil. Make sure your design is flexible enough to allow configuration based tweaking.
Make sure that none of your score constraints cause a score trap. A trapped score constraint uses the same weight for different constraint matches, when it could just as easily use a different weight. It effectively lumps its constraint matches together, which creates a flatlined score function for that constraint. This can cause a solution state in which several moves need to be done to resolve or lower the weight of that single constraint. Some examples of score traps:
If you need 2 doctors at each table, but you're only moving 1 doctor at a time. So the solver has no incentive to move a doctor to a table with no doctors. Punish a table with no doctors more then a table with only 1 doctor in that score constraint in the score function.
2 exams needs to be conducted at the same time, but you're only move 1 exam at a time. So the solver has a disincentive move one of those exams to another timeslot without moving the other in the same move. Add a course-grained move that moves both exams at the same time.
For example, consider this score trap. If the blue item moves from an overloaded computer to an empty computer, the hard score should improve. The trapped score implementation fails to do that:
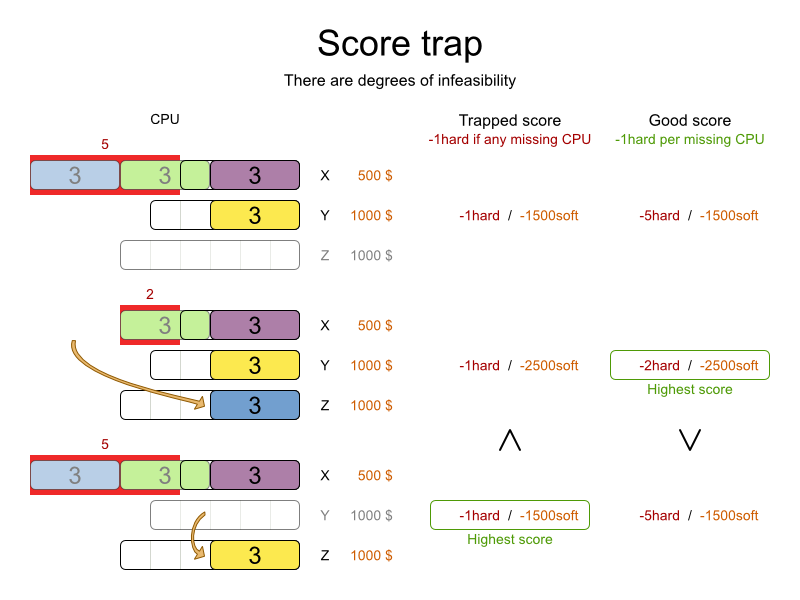
The Solver should eventually get out of this trap, but it will take a lot of effort (especially if there are even more processes on the overloaded computer). Before they do that, they might actually start moving more processes into that overloaded computer, as there is no penalty for doing so.
Note
Avoiding score traps does not mean that your score function should be smart enough to avoid local optima. Leave it to the optimization algorithms to deal with the local optima.
Avoiding score traps means to avoid - for each score constraint individually - a flatlined score function.
Important
Always specify the degree of infeasibility. The business will often say: "if the solution is infeasible, it doesn't matter how infeasible it." While that's true for the business, it's not true for score calculation: it benefits from knowing how infeasible it is. In practice, soft constraints usually do this naturally and it's just a matter of doing it for the hard constraints too.
There are several ways to deal with a score trap:
Improve the score constraint to make a distinction in the score weight. For example: penalize
-1hardfor every missing CPU, instead of just-1hardif any CPU is missing.If changing the score constraint is not allowed from the business perspective, add a lower score level with a score constraint that makes such a distinction. For example: penalize
-1subsoftfor every missing CPU, on top of-1hardif any CPU is missing. The business ignores the subsoft score level.Add course-grained moves and union select them with the existing fine-grained moves. A course-grained move effectively does multiple moves to directly get out of a score trap with a single move. For example: move multiple items from the same container to another container.
Not all score constraints have the same performance cost. Sometimes 1 score constraint can kill the score calculation performance outright. Use the Benchmarker to do a 1 minute run and check what happens to the average calculation count per second if you comment out all but 1 of the score constraints.
Some use cases have a business requirement to provide a fair schedule (usually as a soft score constraint), for example:
Fairly distribute the workload amongst the employees, to avoid envy.
Evenly distribute the workload amongst assets, to improve reliability.
Implementing such a constraint can seem difficult (especially because there are different ways to formalize
fairness), but usually the squared workload implementation behaves most desirable: for each
employee/asset, count the workload w and subtract the square w² from the
score.
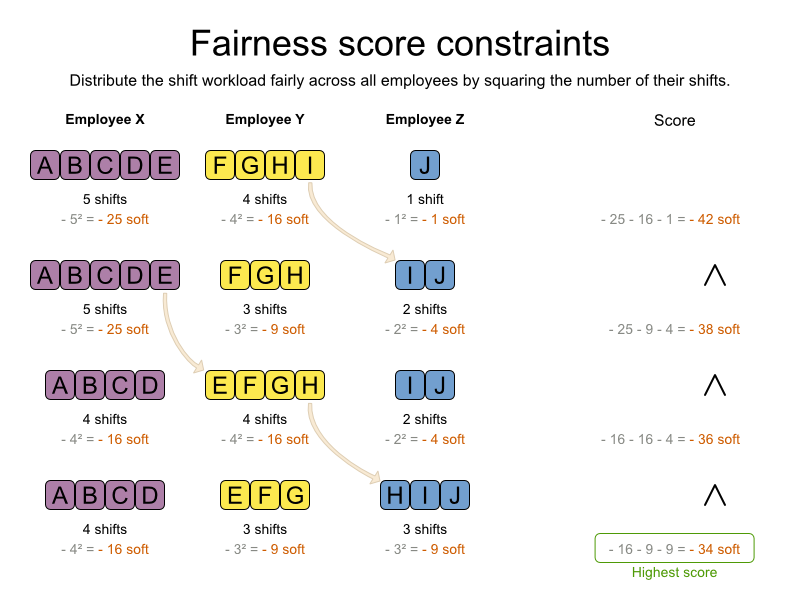
As shown above, the squared workload implementation guarantees that if you select 2 employees from a given solution and make their distribution between those 2 employees more fair that the resulting new solution will have a better overall score.
Other parts of your application, for example your webUI, might need to calculate the score too. Do that by
reusing the ScoreDirectorFactory of the Solver to build a separate
ScoreDirector for that webUI:
ScoreDirectorFactory scoreDirectorFactory = solver.getScoreDirectorFactory();
ScoreDirector guiScoreDirector = scoreDirectorFactory.buildScoreDirector();
Then use it when you need to calculate the Score of a Solution:
guiScoreDirector.setWorkingSolution(solution);
Score score = guiScoreDirector.calculateScore();
To explain in the GUI what entities are causing which part of the Score, get the
ConstraintMatch objects from the ScoreDirector (after calling
calculateScore()):
for (ConstraintMatchTotal constraintMatchTotal : guiScoreDirector.getConstraintMatchTotals()) {
String constraintName = constraintMatchTotal.getConstraintName();
Number weightTotal = constraintMatchTotal.getWeightTotalAsNumber();
for (ConstraintMatch constraintMatch : constraintMatchTotal.getConstraintMatchSet()) {
List<Object> justificationList = constraintMatch.getJustificationList();
Number weight = constraintMatch.getWeightAsNumber();
...
}
}