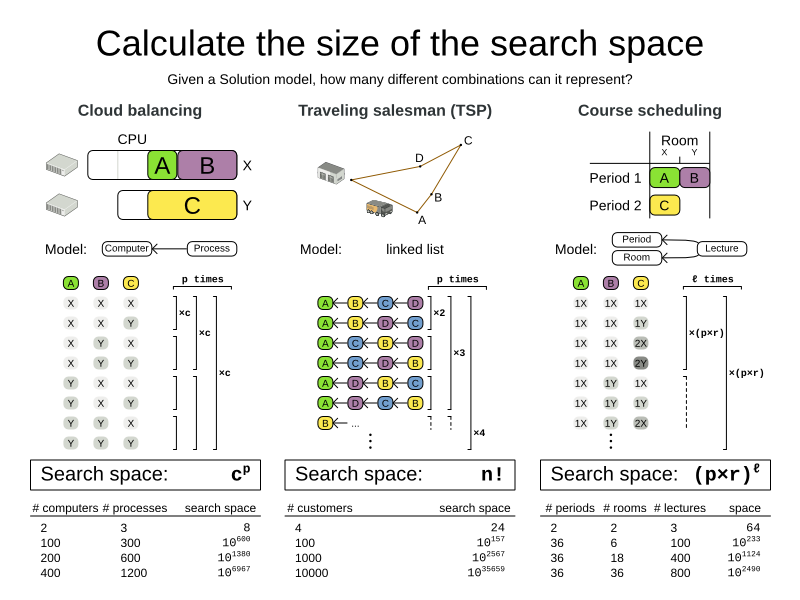
The number of possible solutions for a planning problem can be mind blowing. For example:
4 queens has
256possible solutions (4^4) and 2 optimal solutions.5 queens has
3125possible solutions (5^5) and 1 optimal solution.8 queens has
16777216possible solutions (8^8) and 92 optimal solutions.64 queens has more than
10^115possible solutions (64^64).Most real-life planning problems have an incredible number of possible solutions and only 1 or a few optimal solutions.
For comparison: the minimal number of atoms in the known universe (10^80). As a planning problem gets bigger, the search space tends to blow up really fast. Adding only 1 extra planning entity or planning value can heavily multiply the running time of some algorithms.

Calculating the number of possible solutions depends on the design of the domain model:
Note
This search space size calculation includes infeasible solutions (if they can be represented by the model), because:
The optimal solution might be infeasible.
There are many types of hard constraints which cannot be incorporated in the formula practically. For example in Cloud Balancing, try incorporating the CPU capacity constraint in the formula.
Even in cases were adding some of the hard constraints in the formula is practical, for example Course Scheduling, the resulting search space is still huge.
An algorithm that checks every possible solution (even with pruning such as in Branch And Bound) can easily run for billions of years on a single real-life planning problem. What we really want is to find the best solution in the limited time at our disposal. Planning competitions (such as the International Timetabling Competition) show that Local Search variations (Tabu Search, Simulated Annealing, Late Acceptance, ...) usually perform best for real-world problems given real-world time limitations.
The business wants the optimal solution, but they also have other requirements:
Scale out: Large production datasets must not crash and have good results too.
Optimize the right problem: The constraints must match the actual business needs.
Available time: The solution must be found in time, before it becomes useless to execute.
Reliability: Every dataset must have at least a decent result (better than a human planner).
Given these requirements, and despite the promises of some salesmen, it's usually impossible for anyone or anything to find the optimal solution. Therefore, OptaPlanner focuses on finding the best solution in available time. In realistic, independent competitions, OptaPlanner often comes out as the best reusable software.
The nature of NP-complete problems make scaling a prime concern. The result quality of a small dataset guarantees nothing about the result quality of a large dataset. Scaling issues cannot be mitigated by hardware purchases later on. Start testing with a production sized dataset as soon as possible. Don't asses quality on small datasets (unless production encounters only such datasets). Instead, solve a production sized dataset and compare the results of longer executions, different algorithms and - if available - the human planner.
OptaPlanner is the first framework to combine optimization algorithms (metaheuristics, ...) with score calculation by a rule engine such as Drools Expert. This combination turns out to be a very efficient, because:
A rule engine such as Drools Expert is great for calculating the score of a solution of a planning problem. It makes it easy and scalable to add additional soft or hard constraints such as "a teacher shouldn't teach more then 7 hours a day". It does delta based score calculation without any extra code. However it tends to be not suitable to actually find new solutions.
An optimization algorithm is great at finding new improving solutions for a planning problem, without necessarily brute-forcing every possibility. However it needs to know the score of a solution and offers no support in calculating that score efficiently.
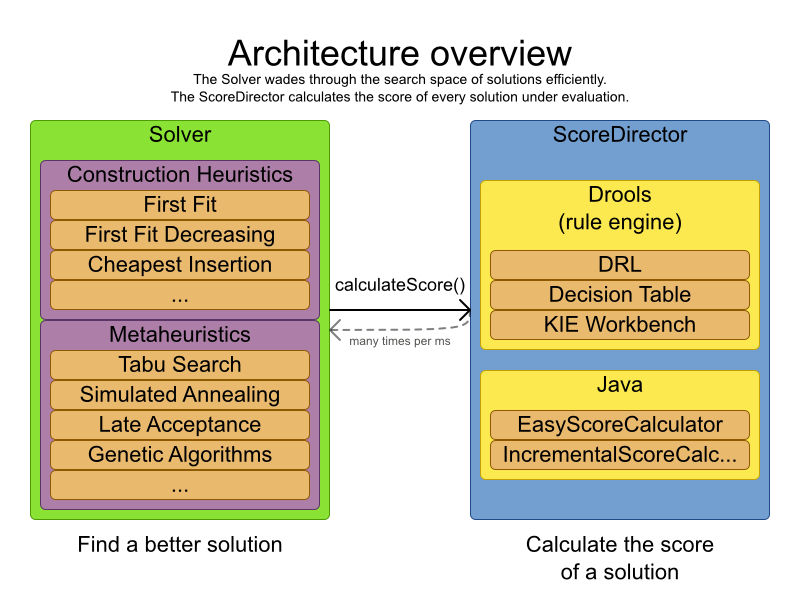
Table 6.1. Optimization algorithms overview
| Algorithm | Scalable? | Optimal? | Easy to use? | Tweakable? | Requires CH? |
|---|---|---|---|---|---|
| Exhaustive Search | |||||
| Brute Force | 0/5 | 5/5 | 5/5 | 0/5 | No |
| Branch And Bound | 0/5 | 5/5 | 4/5 | 2/5 | No |
| Construction heuristics (CH) | |||||
| First Fit | 5/5 | 1/5 | 5/5 | 1/5 | No |
| First Fit Decreasing | 5/5 | 2/5 | 4/5 | 2/5 | No |
| Weakest Fit | 5/5 | 2/5 | 4/5 | 2/5 | No |
| Weakest Fit Decreasing | 5/5 | 2/5 | 4/5 | 2/5 | No |
| Strongest Fit | 5/5 | 2/5 | 4/5 | 2/5 | No |
| Strongest Fit Decreasing | 5/5 | 2/5 | 4/5 | 2/5 | No |
| Cheapest Insertion | 3/5 | 2/5 | 5/5 | 2/5 | No |
| Regret Insertion | 3/5 | 2/5 | 5/5 | 2/5 | No |
| Metaheuristics (MH) | |||||
| Local Search | |||||
| Hill Climbing | 5/5 | 2/5 | 4/5 | 3/5 | Yes |
| Tabu Search | 5/5 | 4/5 | 3/5 | 5/5 | Yes |
| Simulated Annealing | 5/5 | 4/5 | 2/5 | 5/5 | Yes |
| Late Acceptance | 5/5 | 4/5 | 3/5 | 5/5 | Yes |
| Step Counting Hill Climbing | 5/5 | 4/5 | 3/5 | 5/5 | Yes |
| Evolutionary Algorithms | |||||
| Evolutionary Strategies | 4/5 | 3/5 | 2/5 | 5/5 | Yes |
| Genetic Algorithms | 4/5 | 3/5 | 2/5 | 5/5 | Yes |
If you want to learn more about metaheuristics, read the free books Essentials of Metaheuristics or Clever Algorithms.
The best optimization algorithms configuration for your use case depends heavily on your use case. Nevertheless, this vanilla recipe will get you into the game with a pretty good configuration, probably much better than what you're used to.
Start with a quick configuration that involves little or no configuration and optimization code:
Next, implement planning entity difficulty comparison and turn it into:
Next, add Late Acceptance behind it:
First Fit Decreasing
Late Acceptance. A late acceptance size of 400 usually works well.
At this point the free lunch is over. The return on invested time lowers. The result is probably already more than good enough.
But you can do even better, at a lower return on invested time. Use the Benchmarker and try a couple of different Tabu Search, Simulated Annealing and Late Acceptance configurations, for example:
First Fit Decreasing
Tabu Search. An entity tabu size of 7 usually works well.
Use the Benchmarker to improve the values for those size parameters.
If it's worth your time, continue experimenting further. For example, you can even combine multiple algorithms together:
First Fit Decreasing
Late Acceptance (relatively long time)
Tabu Search (relatively short time)
A Solver can use multiple optimization algorithms in sequence. Each
optimization algorithm is represented by a solver Phase. There is never more than 1
Phase solving at the same time.
Note
Some Phase implementations can combine techniques from multiple optimization algorithms,
but they are still just 1 Phase. For example: a local search Phase can do
simulated annealing with entity tabu.
Here's a configuration that runs 3 phases in sequence:
<solver>
...
<constructionHeuristic>
... <!-- First phase: First Fit Decreasing -->
</constructionHeuristic>
<localSearch>
... <!-- Second phase: Late acceptance -->
</localSearch>
<localSearch>
... <!-- Third phase: Tabu Search -->
</localSearch>
</solver>
The solver phases are run in the order defined by solver configuration. When the first
Phase terminates, the second Phase starts, and so on. When the last
Phase terminates, the Solver terminates. Usually, a Solver
will first run a construction heuristic and then run 1 or multiple metaheuristics:
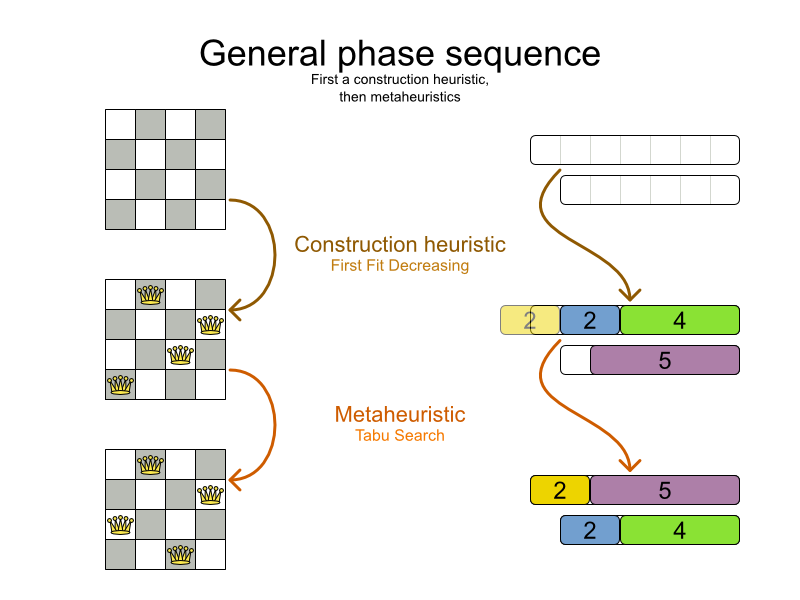
Some phases (especially construction heuristics) will terminate automatically. Other phases (especially
metaheuristics) will only terminate if the Phase is configured to terminate:
<solver>
...
<termination><!-- Solver termination -->
<secondsSpentLimit>90</secondsSpentLimit>
</termination>
<localSearch>
<termination><!-- Phase termination -->
<secondsSpentLimit>60</secondsSpentLimit><!-- Give the next phase a chance to run too, before the Solver terminates -->
</termination>
...
</localSearch>
<localSearch>
...
</localSearch>
</solver>
If the Solver terminates (before the last Phase terminates itself), the
current phase is terminated and all subsequent phases won't run.
A solver will iteratively run phases. Each phase will usually iteratively run steps. Each step, in turn, usually iteratively runs moves. These form 4 nested scopes: solver, phase, step and move.

Configure logging to display the log messages of each scope.
Not all phases terminate automatically and sometimes you don't want to wait that long anyway. A
Solver can be terminated synchronously by up-front configuration or asynchronously from another
thread.
Especially metaheuristic phases will need to be told when to stop solving. This can be because of a number of reasons: the time is up, the perfect score has been reached, ... The only thing you can't depend on, is on finding the optimal solution (unless you know the optimal score), because a metaheuristic algorithm generally doesn't know it when it finds the optimal solution. For real-life problems this doesn't turn out to be much of a problem, because finding the optimal solution could take billions of years, so you 'll want to terminate sooner anyway. The only thing that matters is finding the best solution in the available time.
For synchronous termination, configure a Termination on a Solver or a
Phase when it needs to stop. You can implement your own Termination, but the
build-in implementations should suffice for most needs. Every Termination can calculate a
time gradient (needed for some optimization algorithms), which is a ratio between the time
already spent solving and the estimated entire solving time of the Solver or
Phase.
Terminates when an amount of time has been used:
<termination>
<millisecondsSpentLimit>500</millisecondsSpentLimit>
</termination>
<termination>
<secondsSpentLimit>10</secondsSpentLimit>
</termination>
<termination>
<minutesSpentLimit>5</minutesSpentLimit>
</termination>
<termination>
<hoursSpentLimit>1</hoursSpentLimit>
</termination>
Note
This Termination will most likely sacrifice perfect reproducibility (even with
environmentMode REPRODUCIBLE) because the available CPU time differs
frequently between runs:
The available CPU time influences the number of steps that can be taken, which might be a few more or less.
The
Terminationmight produce slightly different time gradient values, which will send time gradient based algorithms (such as Simulated Annealing) on a radically different path.
Terminates when the best score hasn't improved in an amount of time:
<localSearch>
<termination>
<unimprovedMillisecondsSpentLimit>500</unimprovedMillisecondsSpentLimit>
</termination>
</localSearch>
<localSearch>
<termination>
<unimprovedSecondsSpentLimit>10</unimprovedSecondsSpentLimit>
</termination>
</localSearch>
<localSearch>
<termination>
<unimprovedMinutesSpentLimit>5</unimprovedMinutesSpentLimit>
</termination>
</localSearch>
<localSearch>
<termination>
<unimprovedHoursSpentLimit>1</unimprovedHoursSpentLimit>
</termination>
</localSearch>
This termination should not be applied to Construction Heuristics, because they only update the best
solution at the end. Therefore it might be better to configure it on a specific Phase (such as
<localSearch>), instead of on the Solver itself.
Note
This Termination will most likely sacrifice perfect reproducibility (even with
environmentMode REPRODUCIBLE) because the available CPU time differs
frequently between runs:
The available CPU time influences the number of steps that can be taken, which might be a few more or less.
The
Terminationmight produce slightly different time gradient values, which will send time gradient based algorithms (such as Simulated Annealing) on a radically different path.
Terminates when a certain score has been reached. You can use this Termination if you
know the perfect score, for example for 4 queens (which uses a SimpleScore):
<termination>
<bestScoreLimit>0</bestScoreLimit>
</termination>
For a planning problem with a HardSoftScore, it could look like this:
<termination>
<bestScoreLimit>0hard/-5000soft</bestScoreLimit>
</termination>
For a planning problem with a BendableScore with 3 hard levels and 1 soft level, it could look like this:
<termination>
<bestScoreLimit>0/0/0/-5000</bestScoreLimit>
</termination>
To terminate once a feasible solution has been reached, this Termination isn't practical
because it requires a bestScoreLimit such as 0hard/-2147483648soft. Instead,
use the next termination.
Terminates when a certain score is feasible. Requires that the Score implementation
implements FeasibilityScore.
<termination>
<bestScoreFeasible>true</bestScoreFeasible>
</termination>
This Termination is usually combined with other terminations.
Terminates when an amount of steps has been reached:
<localSearch>
<termination>
<stepCountLimit>100</stepCountLimit>
</termination>
</localSearch>
This Termination can only be used for a Phase (such as
<localSearch>), not for the Solver itself.
Terminates when the best score hasn't improved in a number of steps:
<localSearch>
<termination>
<unimprovedStepCountLimit>100</unimprovedStepCountLimit>
</termination>
</localSearch>
If the score hasn't improved recently, it's probably not going to improve soon anyway and it's not worth the effort to continue. We have observed that once a new best solution is found (even after a long time of no improvement on the best solution), the next few steps tend to improve the best solution too.
This Termination can only be used for a Phase (such as
<localSearch>), not for the Solver itself.
Terminations can be combined, for example: terminate after 100 steps or if a score of
0 has been reached:
<termination>
<terminationCompositionStyle>OR</terminationCompositionStyle>
<stepCountLimit>100</stepCountLimit>
<bestScoreLimit>0</bestScoreLimit>
</termination>
Alternatively you can use AND, for example: terminate after reaching a feasible score of at least
-100 and no improvements in 5 steps:
<termination>
<terminationCompositionStyle>AND</terminationCompositionStyle>
<unimprovedStepCountLimit>5</unimprovedStepCountLimit>
<bestScoreLimit>-100</bestScoreLimit>
</termination>
This example ensures it doesn't just terminate after finding a feasible solution, but also completes any obvious improvements on that solution before terminating.
Sometimes you'll want to terminate a Solver early from another thread, for example because a user action or
a server restart. This cannot be configured by a Termination as it's impossible to predict when
and if it will occur. Therefore the Solver interface has these 2 thread-safe methods:
public interface Solver {
// ...
boolean terminateEarly();
boolean isTerminateEarly();
}
If you call the terminateEarly() method from another thread, the
Solver will terminate at its earliest convenience and the solve(Solution)
method will return in the original Solver thread.
Each time a new best solution is found, the Solver fires a
BestSolutionChangedEvent, in the solver's thread.
To listen to such events, add a SolverEventListener to the
Solver:
public interface Solver {
// ...
void addEventListener(SolverEventListener<? extends Solution> eventListener);
void removeEventListener(SolverEventListener<? extends Solution> eventListener);
}
The BestSolutionChangedEvent's newBestSolution might not be initialized
or feasible. Use the methods on BestSolutionChangedEvent to detect such cases:
solver.addEventListener(new SolverEventListener<CloudBalance>() {
public void bestSolutionChanged(BestSolutionChangedEvent<CloudBalance> event) {
// Ignore invalid solutions
if (event.isNewBestSolutionInitialized()
&& event.getNewBestSolution().getScore().isFeasible()) {
...
}
}
});
Warning
The bestSolutionChanged() method is called in the solver's thread, as part of
Solver.solve(). So it should return quickly to avoid slowing down the solving.
Between phases or before the first phase, you might want to execute a custom action on the
Solution to get a better score. Yet you'll still want to reuse the score calculation. For
example, to implement a custom construction heuristic without implementing an entire
Phase.
Note
Most of the time, a custom construction heuristic is not worth the hassle. The supported constructions
heuristics are configurable (use the Benchmarker to tweak them),
Termination aware and support partially initialized solutions too.
Implement the CustomPhaseCommand interface:
public interface CustomPhaseCommand {
void changeWorkingSolution(ScoreDirector scoreDirector);
}
For example:
public class ToOriginalMachineSolutionInitializer implements CustomPhaseCommand {
public void changeWorkingSolution(ScoreDirector scoreDirector) {
MachineReassignment machineReassignment = (MachineReassignment) scoreDirector.getWorkingSolution();
for (MrProcessAssignment processAssignment : machineReassignment.getProcessAssignmentList()) {
scoreDirector.beforeVariableChanged(processAssignment, "machine");
processAssignment.setMachine(processAssignment.getOriginalMachine());
scoreDirector.afterVariableChanged(processAssignment, "machine");
}
}
}
Warning
Any change on the planning entities in a CustomPhaseCommand must be notified to the
ScoreDirector.
Warning
Do not change any of the planning facts in a CustomPhaseCommand. That will corrupt the
Solver because any previous score or solution was for a different problem. To do that, read
about repeated planning and do it with a ProblemFactChange instead.
Configure your CustomPhaseCommand like this:
<solver>
...
<customPhase>
<customPhaseCommandClass>org.optaplanner.examples.machinereassignment.solver.solution.initializer.ToOriginalMachineSolutionInitializer</customPhaseCommandClass>
</customPhase>
... <!-- Other phases -->
</solver>
Configure multiple customPhaseCommandClass instances to run them in sequence.
Important
If the changes of a CustomPhaseCommand don't result in a better score, the best solution
won't be changed (so effectively nothing will have changed for the next Phase or
CustomPhaseCommand). To force such changes anyway, use
forceUpdateBestSolution:
<customPhase>
<customPhaseCommandClass>...MyUninitializer</customPhaseCommandClass>
<forceUpdateBestSolution>true</forceUpdateBestSolution>
</customPhase>
Note
If the Solver or a Phase wants to terminate while a
CustomPhaseCommand is still running, it will wait to terminate until the
CustomPhaseCommand is done, however long that takes.