|
||||||||||
| PREV CLASS NEXT CLASS | FRAMES NO FRAMES | |||||||||
| SUMMARY: NESTED | FIELD | CONSTR | METHOD | DETAIL: FIELD | CONSTR | METHOD | |||||||||
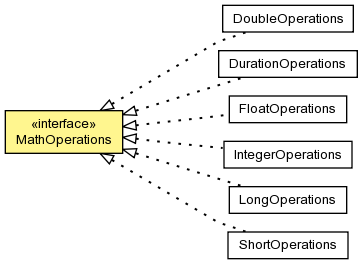
T - the numeric class, usually a subclass of Number (although this is not required)@Immutable public interface MathOperations<T>

The set of mathematic operations for a particular class of values. This is useful for generic classes that must work with one
of the Number subclasses.
| Method Summary | |
|---|---|
T |
add(T value1,
T value2)
Add the two operands and return the sum. |
BigDecimal |
asBigDecimal(T value)
Create a BigDecimal representation of the supplied value. |
int |
compare(T value1,
T value2)
Compare the two operands and return an integer that describes whether the first value is larger, smaller or the same as the second value. |
T |
create(double value)
Convert the double representation into the natural object representation. |
T |
create(int value)
Convert the integer representation into the natural object representation. |
T |
create(long value)
Convert the long representation into the natural object representation. |
T |
createZeroValue()
Create the object form of the "zero value". |
double |
divide(T value1,
T value2)
Divide the first operand by the second, and return the result. |
double |
doubleValue(T value)
Convert the value to a double. |
float |
floatValue(T value)
Convert the value to a float. |
T |
fromBigDecimal(BigDecimal value)
Convert the BigDecimal representation into the natural object representation. |
Comparator<T> |
getComparator()
Return a Comparator for this operand class. |
int |
getExponentInScientificNotation(T value)
Get the exponent if the number were written in exponential form. |
Class<T> |
getOperandClass()
Return the class that these operations operate upon. |
T |
increment(T value)
Increment the supplied operand by 1. |
int |
intValue(T value)
Convert the value to an integer. |
T |
keepSignificantFigures(T value,
int numSigFigs)
|
long |
longValue(T value)
Convert the value to a long integer. |
T |
maximum(T value1,
T value2)
Compare the two operands and return the one that is larger. |
T |
minimum(T value1,
T value2)
Compare the two operands and return the one that is smaller. |
T |
multiply(T value1,
T value2)
Multiply the two operands and return the product. |
T |
negate(T value)
Negate the supplied operand. |
T |
random(T minimum,
T maximum,
Random rng)
Generate a random instance within the specified range. |
T |
roundDown(T value,
int decimalShift)
Round down the supplied value to the desired scale. |
T |
roundUp(T value,
int decimalShift)
Round up the supplied value to the desired scale. |
short |
shortValue(T value)
Convert the value to a short. |
double |
sqrt(T value)
Return the square root of the supplied operand. |
T |
subtract(T value1,
T value2)
Subtract the second operand from the first, and return the difference. |
| Method Detail |
|---|
Class<T> getOperandClass()
T add(T value1,
T value2)
zero value is used in place of any operand that is
null.
value1 - the first operandvalue2 - the second operand
T subtract(T value1,
T value2)
zero value is used in
place of any operand that is null.
value1 - the first operandvalue2 - the second operand
T multiply(T value1,
T value2)
zero value is used in place of any operand
that is null.
value1 - the first operandvalue2 - the second operand
double divide(T value1,
T value2)
zero value is used in place
of any operand that is null.
value1 - the first operandvalue2 - the second operand
T negate(T value)
zero value is used in place of any operand that is null.
value - the value that is to be negated
T increment(T value)
operand class. The zero value is used in place of any operand that is
null.
value - the value that is to be incremented
T maximum(T value1,
T value2)
value1 - the first operandvalue2 - the second operand
T minimum(T value1,
T value2)
value1 - the first operandvalue2 - the second operand
int compare(T value1,
T value2)
Comparable. The zero value is used
in place of any operand that is null.
value1 - the first operandvalue2 - the second operand
BigDecimal asBigDecimal(T value)
BigDecimal representation of the supplied value.
value - the value that is to be converted to a BigDecimal
value is nullT fromBigDecimal(BigDecimal value)
BigDecimal representation into the natural object representation. This may result in loss of some data
(e.g., converting a decimal to an integer results in the loss of the fractional part of the number).
value - the BigDecimal value
value is nulldouble doubleValue(T value)
operand class.
value - the value
float floatValue(T value)
operand
class.
value - the value
int intValue(T value)
operand class.
value - the value
short shortValue(T value)
operand
class.
value - the value
long longValue(T value)
operand class.
value - the value
T createZeroValue()
T create(int value)
value - the integer value
T create(long value)
value - the long value
T create(double value)
value - the double value
double sqrt(T value)
value - the value whose root is to be found; may not be null or 0
Comparator<T> getComparator()
Comparator for this operand class. The implementation is free to
return the same comparator instance from multiple invocations of this method.
int getExponentInScientificNotation(T value)
value - the value
T roundUp(T value,
int decimalShift)
decimalShift places, rounding, and then shifting the decimal point of the rounded value by
-decimalShift
For example, consider the number 10.000354. This can be rounded to 10.0004 by calling this method and supplying the value and an "exponentToKeep" value of -4.
value - the value to be roundeddecimalShift - the number of places the decimal point should be shifted before rounding
T roundDown(T value,
int decimalShift)
decimalShift places, rounding, and then shifting the decimal point of the rounded value by
-decimalShift
For example, consider the number 10.000354. This can be rounded to 10.0003 by calling this method and supplying the value and an "exponentToKeep" value of -4.
value - the value to be roundeddecimalShift - the number of places the decimal point should be shifted before rounding
T keepSignificantFigures(T value,
int numSigFigs)
T random(T minimum,
T maximum,
Random rng)
minimum - the minimum value, or null if the zero-value should be used for the minimummaximum - the maximum value, or null if the zero-value should be used for the maximumrng - the random number generator to use
operand class placed within the desired range using a random
distribution, or null if this class does not support generating random instances
|
||||||||||
| PREV CLASS NEXT CLASS | FRAMES NO FRAMES | |||||||||
| SUMMARY: NESTED | FIELD | CONSTR | METHOD | DETAIL: FIELD | CONSTR | METHOD | |||||||||